Ben MacAdam and Priyaa Srinivasan – The Calgary Peripatetic Seminar

Date: November 10, 2017

Time: 12:00 am - 12:00 am

Location: ICT616

Talk

Talk 1 – Ben MacAdam

Title: Linear/Non-Linear models in a 2-category: Part 1
Abstract:
A linear/non-linear model is a monoidal adjunction between a cartesian category and symmetric monoidal category. Such an adjunction gives rise to a coalgebraic modality which in turn a model of MELL. Birkedal showed that these results translate easily to fibred monoidal categories — here one
obtains a model in each fiber category. We show that many of these results can be further generalized to pseudomonoids in 2-categories with suitable universal properties.

Talk 2 – Priyaa Srinivasan

Title: Structures for decoherent

Abstract:

This talk will introduce and develop the structure required for studying

decoherence in certain monoidal categories. Our driving example is a

decoherence structure in $\mathsf{CP}^*[\mathsf{FHilb}]$

Our goal is to move towards understanding the following:

Theorem:

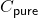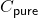Let $C$ be a dagger compact closed category and $C_\mathsf{pure}$ be a subcategory of $C$ that inherits the dagger and compact closed structure. Suppose $C_\mathsf{pure}$ has a decoherence structure with purification, then there exists an invertible dagger functor from $\mathsf{CP}^*[C_\mathsf{pure}] \to C$ such that $F(f \otimes g) = F(f) \otimes F(g)$ .