Cole Comfort and Priyaa Srinivasan (or Priyaa and Cole)

Date: November 24, 2017

Location: ICT616

Talk

Title: A Complete Classification of the Toffoli Gate with Ancillary bits
Abstract:
The Toffoli gate is a universal gate for classical reversible computation. This means that if we are allowed to fix the values of certain inputs and outputs (called ancillary bits), we can simulate any Boolean function from $\mathbb{Z}_2^n \to \mathbb{Z}_2^m$ with a circuit from $n\to m+k$ wires consisting only of Toffoli gates (with $k$ extra ignored outputs).

Iwama found a complete set of identities for circuits solely consisting of Toffoli gates. I present a complete set of identities for the symmetric monoidal category generated by the Toffoli gate \emph{and ancillary bits}. I also provide a normal form for these circuits and prove an equivalence of categories into a subcategory of $\mathsf{PInj}$

Title: Structures for decoherence

Abstract:

This talk will introduce and develop the structure required for studying

decoherence in certain monoidal categories. Our driving example is a

decoherence structure in $\mathsf{CP}^*[\mathsf{FHilb}]$

Our goal is to move towards understanding the following:

Theorem:

Let C be a dagger compact closed category and 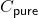$C_\mathsf{pure}$ be a subcategory of C that inherits the dagger and compact closed structure. Suppose 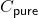$C_\mathsf{pure}$ has a decoherence structure with purification, then there exists an invertible dagger functor $\mathsf{CP}^*[C_\mathsf{pure}] \to C$ such that $F(f \otimes g) = F(f) \otimes F(g)$ .